Параметрическое моделирование: описание, методы, обзор программ

Описание модели стула

В рассматриваемом примере регулируемым параметром является радиус скруглений R между отдельными компонентами модели стула. Изменение радиуса влечет изменение высоты ножек стула, размеров его сиденья и спинки (рис. 3).

Модель имеет следующие характеристики:

1. Радиус всех скруглений одинаков и изменяется с шагом 1 в диапазоне 5 – 15 единиц.
2. При пересчете модели сохраняются габариты стула, хранимые глобальными переменными wX, wY и wZ, а также размеры и положение задних ножек стула.
3. Каркас стула воспроизводится цилиндрами и дугами (примитивы Cylinder и Arc); последние используются для отображения скруглений.
4. Сиденье и списка стула отображаются посредством примитива Plane (плоскость).
5. Сиденье отстоит от основания стула на 0.5 * wZ.

Причины развития этого стиля

На протяжении всей истории развития архитектуры люди стремились возводить здания, которые шли бы в ногу со временем и соответствовали их потребностям (эстетическим и практическим).

В современной архитектуре человек стремится создавать такие проекты, которые сочетали бы в себе много различных функций, предусматривали бы экономически выгодные затраты на их реализацию и в дальнейшем были бы практичны в использовании. Эстетичность и красота отходят на задний план, но эксклюзивность или хотя бы необычность все же преобладают.

У архитекторов современности возникает желание создавать что-то новое, уникальное, то, что имеет в своей основе последние разработки и принципы архитектурных сооружений.

И, как результат, архитектор начинает осваивать новые инструменты для дальнейшей работы – это анимация, параметрическое моделирование, мутация и другие достижения современной компьютерной графики. И только сейчас, с появлением и развитием передовых параметрических дизайнерских систем, параметрическая архитектура оформилась как отдельный стиль и начала приобретать все большую популярность и востребованность.

Источники информации для параметрического дизайна

Параметрическая архитектура целых городов, отдельных строений, параметрический интерьер и дизайн помещений становятся все более доступными не только для всех профессионалов-архитекторов и дизайнеров, но и для смелых владельцев недвижимости. Ведь в скором времени любой желающий может создать предмет мебели или даже дом своей мечты при помощи параметрического моделирования.

Количество учебной литературы в этой области растет и становится все больше доступным для простых обывателей, которым интересна и привлекательна параметрическая архитектура. 3D max, Quest3D Professional и ряд других – это программы моделирования, которые помогают архитекторам создавать параметрические шедевры, упрощаются для пользователей с целью увеличения доступности и понимания.

С помощью целой серии программ по параметрическому моделированию можно создать простые (такие как небольшие предметы интерьера типа стула или лампы) и сложные (целый коттедж или даже городской квартал) объекты.

Книги по параметрической архитектуре дают возможность досконально изучить сами понятия «параметризм», «параметрическая архитектура», их роль в современной архитектуре и имеющиеся прогнозы на будущее в этом направлении.

Главная работа основателя этого течения в архитектуре Патрика Шумахера «Параметризм — Новый глобальный стиль для архитектуры и городского дизайна», вышедшая в 2009 году, детально описывает все аспекты этого направления и его роль в строительстве будущего.

Из русскоязычной литературы можно выделить учебник для вузов в пяти томах Н.Ф. Гуляницкого под названием «Архитектура гражданских и промышленных зданий».

Определение

В литературе нет ясного общего мнения, как следовало бы определить параметрическую редукцию формально и имеется тонкая разница в использовании таких выражений.

Обозначение Дауни — Феллоуза

В обозначениях Дауни — Феллоузапараметризованная задача — это подмножество L⊆Σ∗×N{\displaystyle L\subseteq \Sigma ^{*}\times \mathbb {N} }, описывающее задачу разрешимости.

Параметрическая редукция параметризованной задачи L{\displaystyle L} — это алгоритм, который берёт представителя (x,k){\displaystyle (x,k)} и отображает его за время, полиномиально зависящее от |x|{\displaystyle |x|} и k{\displaystyle k}, в представителя (x′,k′){\displaystyle (x’,k’)}, так что

• (x,k){\displaystyle (x,k)} входит в L{\displaystyle L} тогда и только тогда, когда (x′,k′){\displaystyle (x’,k’)} входит L{\displaystyle L},
• размер x′{\displaystyle x’} ограничен вычислимой функцией f{\displaystyle f} от k{\displaystyle k}
• k′{\displaystyle k’} ограничено вычислимой функцией от k{\displaystyle k}.

Выход (x′,k′){\displaystyle (x’,k’)} параметрической редукции называется ядром. В этом общем контексте размер строки x′{\displaystyle x’} часто называется её длиной.
Некоторые авторы предпочитают число вершин или число рёбер в качестве размера в контексте задач на графах.

Обозначение Флама — Гроэ

В обозначениях Флама — Гроэпараметризованная задача состоит из задачи приятия решения L⊆Σ∗{\displaystyle L\subseteq \Sigma ^{*}} и функции κΣ∗→N{\displaystyle \kappa :\Sigma ^{*}\to \mathbb {N} }, собственно параметризации. Параметр представителя задачи x{\displaystyle x} — число κ(x){\displaystyle \kappa (x)}.

Параметрическая редукция для параметризованной задачи L{\displaystyle L} является алгоритмом, который берёт представителя x{\displaystyle x} с параметром k{\displaystyle k} и отображает его за полиномиальное время в представителя y{\displaystyle y} так, что

• x{\displaystyle x} входит в L{\displaystyle L} тогда и только тогда, когда y{\displaystyle y} входит в L{\displaystyle L}
• размер y{\displaystyle y} ограничен вычислимой функцией f{\displaystyle f} от k{\displaystyle k}.

Заметим, что в этих обозначениях граница размера y{\displaystyle y} подразумевает, что параметр y{\displaystyle y} также ограничен функцией от k{\displaystyle k}.

Функцию f{\displaystyle f} часто называют размером ядра. Если f=kO(1){\displaystyle f=k^{O(1)}} говорят, что L{\displaystyle L} допускает полиномиальное ядро. Подобным образом для f=O(k){\displaystyle f={O(k)}} задача допускает линейное ядро.

Виды и уровни 3D-моделей

Существует несколько видов трехмерных моделей:

• полигональная модель;
• NURBS поверхности.

Вторые имеют более высокий уровень точности, так что их чаще всего используют инженеры, машиностроители и архитекторы. А вот полигональные модели чаще используются для создания 3D-изображений в мультипликации, кинематографе и компьютерных играх. Они состоят из многочисленных простейших геометрических фигур, которые также называют примитивами.

Кроме того, есть три вида 3D-моделирования:

• каркасное моделирование;
• поверхностное моделирование;
• твердотельное моделирование.

Первый из них, наиболее простой вид – это каркасное моделирование. Модели, получаемые при создании этого типа воспроизведения, будут называться проволочными или каркасными. Состоят они из линий, дуг и сегментов. Изображения такого типа не передают полную информацию об объекте: ни об объеме, ни о структуре поверхности из такой модели узнать невозможно, зато можно изучить его устройство и функциональность. Главным преимуществом каркасного моделирования является то, что на хранение трехмерных моделей, созданных этим способом, не требуется много оперативной памяти компьютера. Чаще всего каркасная визуализация применяется в специализированных программах для построения предполагаемой траектории движения устройства или инструмента.

Второй вид 3D-моделирования – это поверхностное моделирование. В отличие от каркасного, здесь имеются не только сегменты, линии и дуги, но и поверхности образующие контур отображаемого объекта.

Ну и последний, самый точный и достоверный тип 3D-моделирования, называется твердотельное моделирование. В результате его использования можно получить настоящий образец готового объекта, который передает все данные о нем. Модель, созданная благодаря этому способу визуального воспроизведения, содержит линии, грани, текстуру и данные об объеме и массе тела. Хотя изображения и занимают наибольший объем памяти компьютера по сравнению с остальными, но он полностью описывает готовый объект. Твердотельное моделирование используется повсюду: при создании техники, промышленных деталей, мебели, ювелирных изделий, кино и компьютерных игр.

Из-за того, что 3D-модели используются практически во всех сферах нашей жизни, можно выделить четыре уровня сложности объемных изображений:

• Первый – простейший – не содержит информации о структуре и мелких деталях объекта, например бокалы и простые рамки.
• Второй, немного более сложный уровень, содержит более детальную информацию о модели. К такому уровню можно отнести тумбы, столы и другие несложные предметы.
• К третьему уровню можно отнести гарнитуры мебели и технику для дома из-за многочисленных мелких деталей и сложной неоднородной структуры.
• Ну а четвертый чаще всего используется инженерами, примерами трехмерных моделей этого уровня могут служить модели станков, автомобилей и другой сложной техники.

Все уровни модели соотносятся и с видами 3D-моделирования, так первые два – это каркасный, третий – поверхностный, а четвертый – твердотельный способ визуализации.

Процесс параметрического моделирования

Модели строятся из набора математических формул и чтобы они имели легитимность, они должны основываться на реальной информации об изделии. Совершенство методов проверки и полнота информации об изделии определяют жизнеспособность решения.

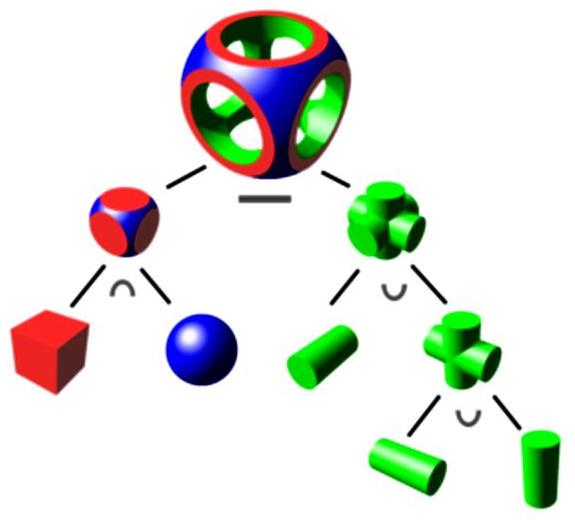
Существует две популярные PM-модели:

1. Конструктивная твердая геометрия (CSG) – определяет модель с точки зрения объединения основных и генерируемых физических форм. Она использует логические операции для построения модели. Это комбинация трехмерных элементарных форм, например, цилиндра, конуса, призмы, прямоугольника или сферы, которыми управляют с помощью простых логических операций.
2. Граничное представительство (BR) – сплошная модель формируется путем определения поверхностей, которые формируют пространственные границы. Затем создается объект путем соединения точек в пространстве. Многие программы используют метод конечных элементов (FEM), поскольку он позволяет легко контролировать внутреннюю сетку объема.

Термин параметрическое 3D моделирование означает, что программа MCAD использует физические данные. В этом методе размеры определяют геометрию, а не наоборот, как в случае 2D и традиционных трехмерных твердотельных моделях. Поэтому любое редактирование значений приводит к изменению размера. Кроме того, отношения или ограничения, используемые для создания элементов изделия, фиксируются и контролируются программой.

Что собой представляет

Параметрическая мебель отличается от традиционных моделей необычной, экзотической формой. Авангардный стиль конструкций исключает четкую геометрию, использование идентичных элементов, акценты на функциональных зонах. Предметы мебели больше напоминают арт-объекты с плавными, перетекающими поверхностями, беспорядочными изгибами. Сложные формы призваны передать красоту природных линий, создать гармоничное, комфортное пространство вокруг человека.

Благодаря особенностям конструкции каждому предмету можно придать оригинальный внешний вид. Мебель напоминает слоеный пирог. Последовательно соединенные детали из фанеры скрепляют металлическими шпильками, оставляя между листами небольшой зазор. В результате получается надежная, устойчивая конструкция.

Индивидуальный подход дает возможность создавать изделия с учетом любых пожеланий. Уже на этапе моделирования можно выбрать дизайн конструкции, увидеть его на экране монитора с привязкой к конкретному интерьеру или месту размещения. К достоинствам подобной мебели относятся ее новизна, эстетическая привлекательность, а также отличные эксплуатационные качества:

• экологическая безопасность;
• функциональность;
• эргономичность;
• прочность конструкции;
• долговечность использования;
• хорошая ремонтопригодность.

Новое направление в дизайне мебели нашло применение при оформлении офисов и торговых центров, кинотеатров, концертных залов, клубов, ресторанов. Беседками, лавками в параметрическом стиле украшают садовые и парковые зоны. По индивидуальным заказам изготавливается мебель для дома или офиса: стулья, кресла, столы, диваны, стеллажи, кровати.

Для создания трехмерных моделей необходимы специальное программное обеспечение, станок ЧПУ, поэтому частные мастера редко занимаются этим непростым делом. Еще один недостаток параметрической мебели — очень высокая стоимость. Ее экзотические формы вписываются не во все интерьеры, особенно не рекомендованы для классических.

Параметрическая редуцируемость и фиксированно-параметрическая разрешимость эквивалентны

Задача является фиксированно-параметрически разрешимой тогда и только тогда, когда её можно параметрически редуцировать и она разрешима.

То, что параметрически редуцируемая и разрешимая задача является фиксированно-параметрически разрешимой, можно видеть из определения выше:
алгоритм параметрической редукции, который работает за время O(|x|c){\displaystyle O(|x|^{c})} для некоторого c, привлекается для получения ядра размера f(k){\displaystyle f(k)}.
Затем ядро решается алгоритмом, который проверяет, что задача разрешима.
Полное время работы этой процедуры равно g(f(k))+O(|x|c){\displaystyle g(f(k))+O(|x|^{c})}, где g(n){\displaystyle g(n)} — время работы алгоритма, используемого для решения ядер. Поскольку g(f(k)){\displaystyle g(f(k))} вычислимо, например, при предположении, что f(k){\displaystyle f(k)} вычислимо, а g(f(k)){\displaystyle g(f(k))} можно вычислить путём перебора всех возможных входов длины f(k){\displaystyle f(k)}, отсюда вытекает, что задача фиксированно-параметрически разрешима.

Доказательство в другом направлении, что фиксированно-параметрически разрешимая задача является параметрически редуцируемой и разрешимой, чуть более трудно. Предположим, что вопрос нетривиален, что означает, что имеется по меньшей мере один представитель задачи с именем Iyes{\displaystyle I_{yes}}, принадлежащий языку, и по меньшей мере один представитель задачи, не принадлежащий языку, с именем Ino{\displaystyle I_{no}}. В противном случае замена любого представителя пустой строкой является допустимой параметрической редукцией. Предположим также, что задача является фиксированно-параметрически разрешимой, то есть она имеет алгоритм, работающий максимум за f(k)⋅|x|c{\displaystyle f(k)\cdot |x|^{c}} шагов на представителях задачи (x,k){\displaystyle (x,k)} для некоторой константы c{\displaystyle c} и некоторой функции f(k){\displaystyle f(k)}. Для осуществления параметрической редукции входа применяем алгоритм на заданном входе за максимум |x|c+1{\displaystyle |x|^{c+1}} шагов. Если алгоритм завершается ответом, используем ответ для выбора либо Iyes{\displaystyle I_{yes}}, либо Ino{\displaystyle I_{no}} в качестве ядра. Если, вместо этого, достигаем границы число шагов |x|c+1{\displaystyle |x|^{c+1}} без прерывания, возвращаем саму задачу (x,k){\displaystyle (x,k)} в качестве ядра. Поскольку (x,k){\displaystyle (x,k)} возвращается в качестве ядра для входа сf(k)⋅|x|c>|x|c+1{\displaystyle f(k)\cdot |x|^{c}>|x|^{c+1}}, отсюда следует, что размер полученного таким образом ядра не превосходит max{|Iyes|,|Ino|,f(k)}{\displaystyle \max\{|I_{yes}|,|I_{no}|,f(k)\}}. Граница размера вычислима в предположениях фиксированно-параметрической разрешимости, что f(k){\displaystyle f(k)} вычислима.

Параметрика в дизайне интерьера

На данное время этот стиль только начинает свое развитие, которое бурно прогрессирует. Большая часть работ дизайнеров этого направления направлена на торговые центры, рестораны, галереи, музеи и другие коммерческие сооружения.

Параметрическая архитектура в интерьере частного жилья развивается намного медленнее, причиной тому является потребность в больших габаритах, поскольку параметризму нужен определенный размах и большая площадь для чувства максимального комфорта находящихся в помещении людей.

Этот новый стиль в интерьере позволяет сделать его более спокойным, плавным и менее брутальным чем, к примеру, стили кантри или прованс.

Параметрическими возможно сделать потолок, стены, перестенки, мебель и элементы декора.

Часто для интерьера в параметрике используют природные материалы. Это в основном дерево и камень, которые создают ощущение комфорта и уединения, помогают спрятаться от суеты большого города.

Из цветов преобладают спокойные и классические тона белого, черного, слоновой кости, серого и коричневого, также много оттенков дерева.

Этот стиль характеризуется плавными линиями, перетекающими и струящимися, подобно ткани.

Все элементы декора и мебель в параметрике имеют просто фантастический, космический вид, в котором стираются четкие грани и прямые углы.

Параметрический дизайн выделяется из всех остальных стилей возможностью создания таких архитектурных объемов и элементов, которые раньше казались чем-то нереальным и невыполнимым. Главными причинами этого были сложность и дороговизна выполнения таких объектов. Интерьер в таком стиле смотрится, как открытка из будущего.

Параметризм в помещениях уникален, он практичен и многофункционален.

Многофункциональность параметризма

Отличительной чертой этого течения в дизайне является многофункциональность ее отдельных элементов. Это достигается благодаря мягкому переходу линий в тригонометрическом пространстве и их пересечению.

К примеру, стена может одновременно служить и скамейкой или стулом. А столик, выполненный в этом стиле, может служить одновременно и небольшой этажеркой при помощи нескольких ниш, которые сформировались вследствие переплетения линий.

Так отделывают даже внутренние стены помещения, создавая иллюзию расширения пространства, благодаря отсутствию прямых линий и объемности поверхностей.

Компьютерная генерация модели

В более узком смысле, термин CAD – это компьютерная генерация и модификация геометрической модели. В более широком смысле – включает все автоматизированные действия в процессе проектирования: геометрическое моделирование, вычисление, сбор и предоставление информации от разработки концепции до изготовления.

Изначально приложения использовались для разработки производственных документов. С увеличением вычислительной мощности системы со сложными экспертными приложениями и интегрированными решениями, FEM стал более часто применяться для проектирования и создания продукта. Доступна конструкция технических решений, благодаря которой объекты с самого начала рассматриваются, как трехмерные тела. При необходимости, технические чертежи создаются автоматически из виртуальных моделей деталей.

Особое преимущество 3D-CAD – это возможность проектировать изображение изделия с любого направления. 3D принтер позволяет перейти от виртуального к реальному объекту. Вместе с обнаруживаемыми свойствами материала создаются усовершенствованные модели для заданных физических свойств, например, прочности, упругости. CAD используется практически во всех отраслях техники: архитектуре, гражданском строительстве, машиностроении, электротехники и таких узких направлениях, как стоматологические технологии.

Возникновение и основатели этого стиля

Изначально возникло отдельное направление – параметризм, а уже спустя некоторое время на его основе сформировалась самостоятельная параметрическая архитектура. Заха Хадид – британский архитектор, которая имеет арабские корни, считается одним из основателей этого течения в современной архитектуре. Она еще в начале 1980-х годов в своей мастерской создавала проекты в новом необычном стиле, таком удивительном на то время. Партнером легендарной Захи Хадид был Патрик Шумахер. Именно эти два архитектора ввели новый свежий и необыкновенный поток в застоявшийся без изменений архитектурный мир.

Параметризм на данное время начал охватывать все более обширные сферы архитектуры, строительства и дизайна интерьеров.

Философия параметризма от Патрика Шумахера.

Каждый период в архитектуре основан на предыдущем стиле:  готика, барокко, рококо, модернизм, конструктивизм и другие. Каждый стиль зависит от технологии строительной индустрии того времени.
В процессе развития архитектуры, человек стремится создавать объекты, которые обладают многофункциональными свойствами. Предпочтения отдаются проектам, которые не эстетичны и эксклюзивны, но экономичны и практичны.

Патрик Шумахер, нынешний глава ZHA, продвигает параметризм не только как метод дизайна, но и как философский и стилистический преемник модернизма. Как и принципы Шумахера, принципы параметрического проектирования становятся обычным явлением в практической архитектуре. Функции систем автоматизированного проектирования, таких как Revit или Archicad, позволяют контролировать элементы проекта, посредством связи переменных и учитывать рациональные изменения в качестве ответной реакции на перемены в разных частях проекта.

Независимо от мнения о параметризме как стиле, архитекторы во всем мире должны принимать параметрический дизайн именно за его рациональность.

Зачастую архитекторы применяют параметрику как стилистическое направление, вместо рационализации строительства и производства. Эстетическая известность иногда является одним из требований клиента и часто является аспектом именно дизайна, в который архитекторы вносят больший вклад. Архитекторы, такие как Сантьяго Калатрава часто выбираются  прежде всего из-за, поразительного характера его работ.

Кривые таких зданий соответствуют программе и назначению этих сооружений, которые практически невозможно создать не прибегая к параметрическому программному моделированию. В этом смысле эстетика связана с философией дизайна.

 Тем не менее, связь обеспечиваемая параметрическим проектированием, также присуща более качественному дизайну. Взаимная изменчивость всех элементов дизайна позволяет использовать параметрические инструменты для визуализации того, как изменения в таких параметрах как размер и расположение комнат, будут влиять на такие аспекты, как построение оболочки и внутренняя циркуляция воздуха. Эти аспекты проекта могут быть учтены на раннем этапе в процессе проектирования, чтобы устранить потенциальные проблемы в любой части проекта, как только они появятся.

Параметрическая архитектура – это вовсе не мимолётный тренд, а устойчивое развивающееся направление в современной цифровой, или как пишут в журналах, дигитальной архитектуре.

 Одним из наиболее очевидных преимуществ параметрической архитектуры является экономия. Процесс параметрического проектирования имеет огромный потенциал для экономии времени и денег, благодаря его способности автоматизировать изменения в модели здания и рабочей документации. Такие программы как Revit уже включили такую ​​автоматизацию, позволяя изменять несколько элементов (например, типы дверей и окон), изменяя переменную, контролирующую высоту, ширину или материал.

Материалы и расцветки

Основой для многослойной мебели служат детали из древесины и листовых материалов. Наиболее популярны фанера из различных пород дерева, композитные плиты МДФ, оргстекло и гораздо реже ЛДСП. Подбор сырья связан с особенностями конструкции и назначением мебели:

1. Для уличных объектов важны водоотталкивающие свойства, поэтому предпочтение отдают березовой фанере.
2. Для внутренних помещений подходят массив или фанера из хвойных пород деревьев.
3. Предметы мебели под покраску изготавливают из МДФ (мелкодисперсионной фракции). Материал прочный, хорошо удерживает крепеж.
4. ЛДСП (ламинированная древесно-стружечная плита) не отличается высокой прочностью, поэтому используется для легких, простых конструкций или отделки.

При изготовлении мебели из природного материала стараются подчеркнуть его красоту. Чаще всего сохраняют текстуру и натуральный оттенок древесины от светлых до темных тонов. Популярна цветовая гамма от белого до всех оттенков серого, черные и красные лакированные поверхности. Чтобы подчеркнуть достоинства материала, применяют принцип контраста. Используют столешницы из стекла, пластика или эффектную подсветку, чтобы показать оригинальность конструкции.

Березовая фанераМассив сосныМДФЛДСП

Описание программы

Построение стула обеспечивает функция mkChr, которая принимает в качестве параметров значения радиуса скруглений, длину, ширину и высоту стула – это соответственно параметры R, wX, wY и wZ. Стул состоит из 11 цилиндров (примитив Cylinder), 8 дуг (примитив Arc) и двух плоскостей (примитив Plane). Последние употребляются для отображения сиденья и спинки стула.
Переменные wX, wY и wZ объявлены как глобальные, что позволяет применять их в обработчике on btnNmt pressed управляющего диалога Chair (идентификатор rChr).
Цилиндры хранит массив arrC; номера цилиндров, то есть их индексы в массиве arrC, показаны на рис. 5, а.

Дуги хранятся в массиве arrRc; их индексы в этом массиве показаны на рис. 5, б.
Плоскости для сиденья и спинки имеют в программе соответственно идентификаторы pln и pln2. Эти имена являются глобальными и поэтому доступны в обработчиках диалога Chair.
Перед построением модели функцией Prps удаляются все элементы сцены и устанавливаются требуемые параметры сеанса – это тип единиц измерения, число видовых портов (4), активный видовой порт (4) и его тип (Perspective). Кроме того, в этом видовом порте устраняется изображение сетки и выполняется команда max tool zoomExtents.
Координаты базовых точек цилиндров и дуг вычисляются соответственно функциями fndPs и fndPs2, принимающими вдобавок к параметрам R, wX, wY и wZ соответственно массивы arrPs и arrPs2. В эти массивы названные функции записывают необходимые для построения примитивов координаты их базовых точек. Нумерация базовых точек отвечает показанным на рис. 5 нумерациям цилиндров и дуг.
Параметризация модели обеспечивается функцией chgChr, которая вызывается обработчиком on spnR changed при изменении счетчика R (spinner spnR) диалога Chair. Также эта функция применяется при создании ключей анимации (кнопка Animation диалога Chair).
Функция принимает параметры R, wX, wY и wZ. Параметр R является изменяемым, и его значение берется равным показанию счетчика R диалога. Прочие параметры после запуска программы не изменяются.
Получив новое значение радиуса, функция chgChr:

• изменяет высоту цилиндров 1 и 2 (свойство Height цилиндра);
• соответствующим образом масштабирует цилиндры 5 – 9 (свойство Scale цилиндра);
• изменяет положение цилиндров 9, 10 и 11 (свойство Pos цилиндра), смещая позицию цилиндров 10 и 11 в начало, а цилиндр 9 в конец соответствующих дуг модели;
• изменяет координаты центра каждой дуги (свойство Pos дуги); для этой цели, как и при создании модели, выполняется обращение к функции fndPs2;
• изменяет значение радиуса каждой дуги (свойство Radius дуги);
• модифицирует ширину сиденья и спинки (свойство Width плоскостей pln и pln2).

В рассматриваемой модели масштабирование цилиндра будет вызывать надлежащий эффект, если базовая точка цилиндра (свойство Pivot) расположена в его центре, а не в центре основания, как это предусмотрено по умолчанию. Эта проблема решается при создании модели функцией mkChr за счет употребления следующего кода:

for k = 5 to 9 do arrC.Pivot = .Height]

Таким образом, функция chgChr обеспечивает получение экземпляра модели, отвечающего принятому функцией значению радиуса скругления R. Все преобразования выполняются исходя из неизменности габаритов стула и положения его сиденья. Единственными неизменяемыми компонентами модели являются цилиндры 3 и 4, отображающие задние ножки стула.
Кроме обработчика on spnR changed, вызываемого при изменении показания счетчика R, диалог Chair (см. рис. 4) содержит обработчики on theClr changed, on btnNmt pressed и on btnCls pressed do, выполняемые соответственно при нажатии на полосу с цветом (элемент colorPicker), на кнопку Animation (элемент button btnNmt) и Close (элемент button btnCls).
Ключи анимации рассчитываются в точках 0f, 50f и 100f временной шкалы после нажатия на кнопку Animation диалога Chair: выполняется обработчик on btnCls pressed do, в котором трижды вызывается функция chgChr. После воспроизведения анимации (метод playAnimation) временная шкала устанавливается в точку 0f и вновь вызывается функция chgChr со значением параметра R, равным 10. Это обеспечивает появление начального образа стула. Это же значение радиуса скругления устанавливается и в счетчике R диалога (spnR.Value = 10).